HTB BUSINESS CTF: CRYPTO CHALLENGE – BLINDED

This blog post was written by Varun Gupta.
Introduction
This blog will cover on how to solve the Crypto Challenge – Blinded, which was part of HTB Business CTF. This challenge was based on the RSA algorithm and specifically the Blind Signature concept of RSA. First, let us discuss what the RSA algorithm is and how it works.
What is RSA Algorithm
The RSA algorithm is an asymmetric cryptography algorithm; it uses a public key and a private key (i.e., two different, mathematically linked keys). As their names suggest, a public key is shared publicly, while a private key is secret and must not be shared with anyone.
The RSA algorithm is named after those who invented it in 1978: Ron Rivest, Adi Shamir, and Leonard Adleman.
The following illustration highlights how asymmetric cryptography works:

How does RSA Works?
The following steps outline how the RSA algorithm actually works:
Generating the Keys
- Select two large prime numbers, p and q. The prime numbers need to be large so that they will be difficult for someone to figure out.
- Calculate n = p * q
- Calculate the totient function; ϕ (n) = (p-1) (q-1)
- Select an integer e, such that e is co-prime to ϕ(n) and 1 < e < <ϕ(n). The pair of numbers (n,e) makes up the public key. Note: Two integers are co-prime if the only positive integer that divides them is 1.
- Calculate d such that e.d = 1 mod ϕ(n). d can be found using the extended Euclidean algorithm. The pair (n,d) makes up the private key.
Encryption
Given a plaintext P, represented as a number, the ciphertext C is calculated as:
C = P^e mod n
Decryption
Using the private key (n, d), the plaintext can be found using:
P = C^d mod n
Example
For the sake of simplicity, let us select two small prime numbers:
p = 2
q = 7
Then we calculate n by:
n = p * q
n = 7 * 2
n = 14
Then we calculate ϕ(n) by:
ϕ(n) = (p−1) (q−1)
ϕ(n) = (2−1) (7−1)
ϕ(n) = 6
Then we select e, which is a co-prime to ϕ(n). In our case:
e = 5
Then we calculate our d using the Euclidean algorithm (you can go research on this further):
d = 11
We can confirm that it is the correct figure by using:
e.d mod ϕ(n) = 1
5 * 11 mod 6 = 1
55 mod 6 = 1
As the remainder of 55 divided by 6 is 1, we can use d = 11.
Therefore, our public and private keys are:
Public Key = (14, 5)
Private Key = (14, 11)
Let us take an example of Varun wants to send an encrypted message to Amarjit. Varun has Amarjit’s public key:
Amarjit’s Public Key = (14, 5)
Varun wants to send the message, P = 2
Varun will first encrypt the message using Amarjit’s Public Key:
P = 2
C = P^e mod n
C = 2^5 mod 14
C =32 mod 14
C = 4
Varun will send C = 4 to Amarjit. Amarjit will then use his own Private Key to decrypt the message:
Amarjit’s Private Key = (14, 11)
Varun’s Transmission, C = 4
P = C^d mod n
P = 4^11 mod 14
P = 4194304 mod 14
P = 2
As you can see, Amarjit successfully received the intended message, P = 2, from Varun.
What is a Blind Signature?
Now that we have understood what RSA is, let us look at the main concept of the challenge, which is Blind Signature.
A blind signature scheme is a type of digital signature that conceals the identity of the message contents and the sender.
In these schemes, the sender’s message is concealed — or blinded — before the recipient signing it. After the recipient signs the blinded message, the sender receives the signed blinded message. The sender can remove the blinding factor to remain with the signed original message. Blind signature schemes are beneficial in applications where information on the sender is an essential communication feature.
Electronic voting is a real-world example of a blind signature scheme is a properly functioning electronic voting system. In this example, the sender (voter) and the signer (recipient, voting authority) are unrelated, and the sender’s personal privacy and voting preference are paramount. The signature is considered valid enough to warrant the vote being recorded with confidence, and the voter remains anonymous.
Going further, should the voting authority be called upon to validate the information they received, they can validate the message’s authenticity but cannot connect it with the sender (called unlinkability).
The CTF Challenge
Now onto the fun part of the blog. Let us see how we can solve the challenge.
The source code given for the challenge is:
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
from math import gcd
e = 0x10001
while True:
p, q = getPrime(1024), getPrime(1024)
if gcd(p-1, e) == 1 and gcd(q-1, e) == 1: # Make sure the parameters are valid.
break
n = p * q
d = pow(e,-1,(p-1)*(q-1))
pubkey = (n, e)
privkey = (n, d)
to_sign = b’Hello, I am an admin of this server’
def sign(message, privkey):
n, d = privkey
return pow(message, d, n)
def verify(message, signature, pubkey):
n, e = pubkey
if pow(signature, e, n) == message:
return True
else:
return False
menu = “””
[1] Sign a message
[2] Verify access to this server
[3] Exit
“””[1:]
def main():
print(“Welcome to the Automated Admin Message Signer. If you are not the admin, please disconnect immediately.”)
print(f “The public key being used by this server is {pubkey}”)
while True:
print(menu)
try:
option = int(input(“Enter your option: “))
if option == 1:
message = int(input(“Enter your message to be signed as an integer: “))
if (message % n) == bytes_to_long(to_sign):
print(“Sorry, you cannot sign the admin message. This incident has been reported.”)
exit(0)
else:
print(f”Signature for {long_to_bytes(message)}: {sign(message, privkey)}”)
elif option == 2:
message = int(input(“Enter your message as an integer: “))
signature = int(input(“Enter your signature for that message as an integer: “))
if verify(message, signature, pubkey):
if long_to_bytes(message) == to_sign:
print(“Access granted. Welcome, admin.”)
print(open(“flag.txt”).read())
exit(0)
else:
print(“Signature valid. Message does not equal admin message however. Access denied.”)
elif option == 3:
print(“Goodbye.”)
exit(0)
else:
print(“Option is not in available options.”)
except Exception as e:
print(“An error occurred when trying to retrieve your input, please try again.”, e)
main()
In this challenge, the p and q values are very large prime numbers generated randomly. The e value is in hexadecimal, which, if converted into a decimal value, will be e = 65,537. We are supposed to get the message and input the signature of the message to get our flag.
The message was already given in the python code as ‘Hello, I am an admin of this server’
However, we need the message in an integer form. To achieve this, I just took parts of the source code and ran it to get the message in integer form. The code which I came up with is as follows:
from Crypto.Util.number import bytes_to_long
message = b’Hello, I am an admin of this server’
message_int = bytes_to_long(message)
print(“The message in integer form is: “)
print(message_int)
This code gave me the message in integer form as:
549382100789656197335916883130352377897969772664197648478433607363964882689830839666

When I try to verify access to the server, it asks me for the signature of the message.
When I try to put a random signature, then it does not do anything and loops back to giving me options to choose again, as shown below:
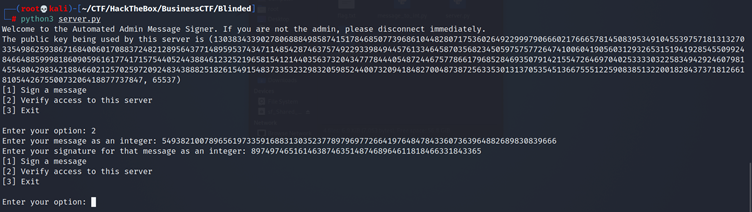
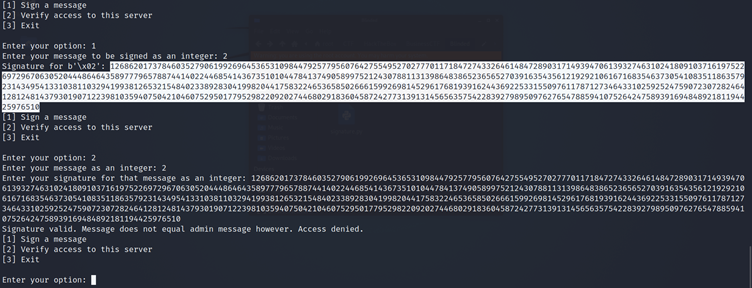
If I try to sign another message and choose option 2 to verify access, and then put the message and correct signature for that message, then I get the following:
If I tried to Sign the Admin Message, which I converted into an integer, I got the following warning:
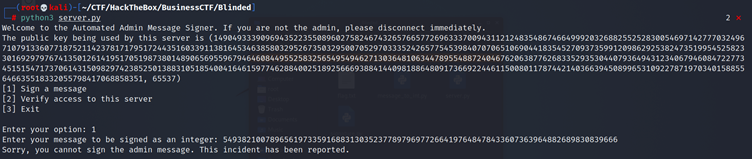
However, I am able to sign multiple messages, as shown below:
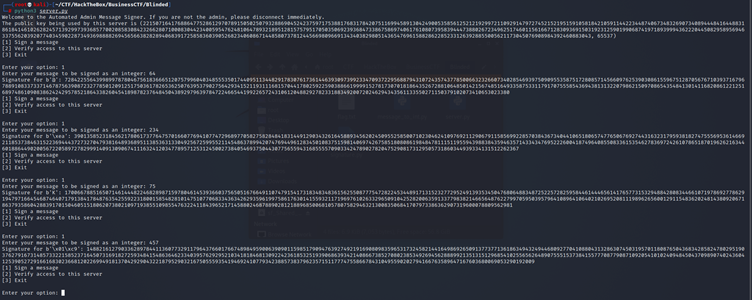
This got me thinking. I can maybe get the different factors of the message, sign them, multiply them together and perform a modulo operator on the result to get the signature of the admin message.
Hence, I got to work. I went to http://www.factordb.com/ to get factors of 549382100789656197335916883130352377897969772664197648478433607363964882689830839666. The factors are as follows:
2, 43, 7994309, 222719525896010669117833, 6602484003938565188377817, 543412310243632685457255119

I then took the above factors one by one and signed them as below:
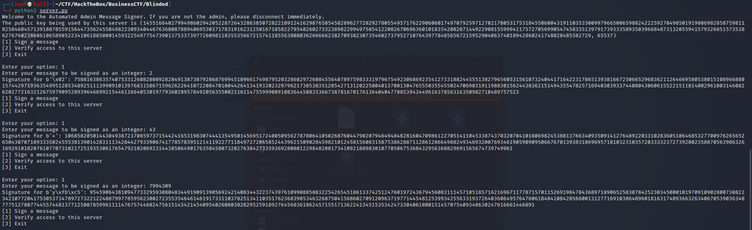
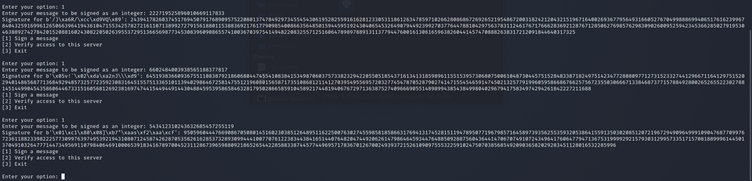
I got the following script from the internet and used it to get the signature of the admin message. I put the signature values of the factors in the script as well:
from pwn import *
from Crypto.Util.number import *
n = 14551664027994986029420522872643286385072822189124162987658545828962772829278055495717622906060174970792597127021780531753184550600431911035330099796650065988242225927049850191980698285875981182584604571391887855915644735624550498223093404467636808788940695303717831916231250167185822795482602733238982299497585412208267069636010183542082871449229081559994117572705699054745833513979173933358935039668487313205594157932685157353862767602386061065890522341061885000145932254977547390137533739772609811835535667215741185563808036266666238270938230735460273795271076439778485656721595290406374018942860241748028485582729
a1 = 7588163863574075331260828089282849138738792868769945189661749879520328602972608455640789759833319796754923068692354127331882445551382796560531561073240441716422317865139381667250665296836211264669580538015108966880157442971936354995128534892511139909101397683158671596262264107220847010044264134193202329796217385383512854271312022580401370013047655503554550247069031911988301562443836215149435547825716940303933744080430606155221511814002961003146082620277216321267597909528939646699215446116640530197793602895784920563550021161147559990091083644508353667387816701761364040477085394344961637856316350982710489757523
a2 = 10685820501443049387237085973715442416531983074441354950145695172400509562787806410502687604479020794649484828160470986122705141104533874370320704101806982453881376634093509141276489220331028360510646853277009762656526504307071893335024555381390142831113428442793390674177857839512141192277118497272065852443962150902845982101245815608315875386288711286128664988249346932007693461905909095066767013938318696957181032310357203333237273920023588705639863261692910182076107707310217251935306176547921020692314438506490176358458073202763842733593692808012298482001734109218898301077050675368432956368829691565674739749961
a3 = 9545906438109477332959308048344919091390569242140834432237439761099088588322542654518613374251247601972436794560831114571051857162169671177871570115269198478436897189065258307842523034500010197091090280073082234210772041753053734789727322122488799778595623002723553546461461917331103782513411035176236839853463268750415686027091209637197714454812539934255633193726403606495764760618484108428566001312771691038648960181631748936632634067053903634877751278077445574481377125007859961111476757446824756151434214540954026080382829525918927645683618624571551713622413451535342473304061800151457075409348630247616661446891
a4 = 2439417826037451769450791768909575220801374784929734554543061952825591616281233053118612634785971026628086867269265219548672003182421204321519671640026936779564931660527670499888699406517616239967840432591699612650663964194361047155342578272161107138992727915618801153883692176177909854008663564850159445951924304065453264907944923992703776447881042975637831124617671766628369212876712850627698576298309026009525942345366285027919530463889274278420152088160243082205026395537295136656987734530839609086557410036703975414948220832557125160647898978891311377944760016130616596382604414574708882638317212091844640317325
a5 = 6451938366093675511083879218606804474554108384153498706037573382329422055051854371613413185989611551539573068075006104873044575152848338718249751423477280809771273152332744129667116412975152029401486568771368492948573257723592308316451557513365101139402986467258147551219608015658717351086812114127039549556957203277454787052879027414715545465914745021325779199605958668676625756723550306667133846873771578849280026526552230278814514499045435860644673315160568126923816974744154494491443048845953958658463281795028665859104589217448194067672971363875274096669055148989943854384998040296794175834974294261842227211688
a6 = 950596044476690867050801451602303851264895116225007630274559858185866317694131745281511947895077196798571645897393562553593205386415591350302085120721967294909649991090476877099767236118823398222577309976397495392194310807124587426287053582616285373289309944410077076122383443841651440764820474492062614798646459344764885092887560436441470670749107243496417606477947136753199992921579303129957335171570818899961445013704910326477714473495691107984064691000653918341678970045231128673965988092186526544228588338744577449695717836701267002493937215261090975553225910247507038568549209036582029283451128016532285996
result = (a1 * a2 * a3 * a4 * a5 * a6) % n
print (“Signature of the admin message is:”)
print (result)
When I ran the script, I got the signature of the admin message as:
4564521452393163432266443543847890995193351723200676930201790269333406530196434696475948952397969375437991659600566954010690775441707088052567176905226755564825909961863893601223820152293623375431168573190461105031364264563948906003963890993950434060516716886292097115738934247400686412991233448245767314611702310599138005425293037245098956708694489499890396228525860874794626437648696465102839889775740344881304092066206104832535374017691400235873603338044998690961341252762822582761019826468052916676862237545668162158131628162156830332879542238588947495594832601869000938988243566076947003244920826813425895526955

I then took this signature and put it in the program:

And VOILA! I got the flag!!
References
https://www.geeksforgeeks.org/rsa-algorithm-cryptography/
https://blog.bi0s.in/2019/03/31/Crypto/Digital-Signatures/volga-quals19-blind/
Disclaimer
The MacroSec blogs are solely for informational and educational purposes. Any actions and or activities related to the material contained within this website are solely your responsibility. The misuse of the information on this website can result in criminal charges brought against the persons in question. The authors and MacroSec will not be held responsible in the event any criminal charges be brought against any individuals misusing the information in this website to break the law.